jupter notebookの使い方

jupter notebook

jupter notebookの起動

jupter notebookの使い方を最低限学んでおく必要があります。簡単に説明するため、あまり画像を用いないで説明します。
とりあえず起動しましょう。
Windowsボタン→Anaconda→Anaconda Navigatorを起動。
jupter notebookのLaunchをクリックします。
jupter notebookが起動したら、AnacondaProjectsフォルダに移動。
右上のNew→Folderで新しい作業用をフォルダを作成。
同じくNew→Python3から実行ファイルを作成します。

jupter notebookの使い方

無事に起動が出来たら、実際にコードを書いていきましょう。

下のようなコードを書いてみましょう。

  print("Hello World!")

実行するにはいくつかの方法がありますが、1番よく使うのはShift+Enterです。 これは、実行と同時に新しい入力を受け付けます。
（他にCtrl+Enterで実行する方法がありますが、この方法だと実行と同時に新しい入力を受け付けることができません。そのときは、左上にある+ボタンがあるので、そこで新しい入力セルを作成できます。）

実行したら下のようになったと思います。

f:id:ShogoAkiyama:20170907203820p:plain

なお、下のように何かしらのエラーが発生したとします。そのときは、エラーを修正して、もう一度Shift+Enterをすれば、実行できます。 この場合はprintf→printに直せばいいことになります。

f:id:ShogoAkiyama:20170907204108p:plain

他の機能としては、複数行書きたいときはEnterで改行していきます。
途中の行に追加したくなったときは、上にある+ボタン。
行を削除したくなったときはその横のカットボタン(ハサミマーク)を使えば良いでしょう。

最低限の機能と使い方は説明したので、あとは実際に使いながら学びましょう。

Pythonの基本 http://shogoakiyama.hatenablog.com/entry/2017/09/07/223357

ディープラーニングを始めるための環境構築

環境構築

ディープラーニングでは主にPythonが使われます。そのための環境構築を行っていきます。

Anacondaのインストール

AnacondaはPythonを含め、ディープラーニングで必要となるパッケージを一括でインストールすることができます。 また、Pythonの仮想環境を簡単に作成することができるので、プロジェクトに応じて必要な環境を構築することができます。 Anacondaは下のサイトからインストールします。

https://www.anaconda.com/download/

f:id:ShogoAkiyama:20170906232103j:plain

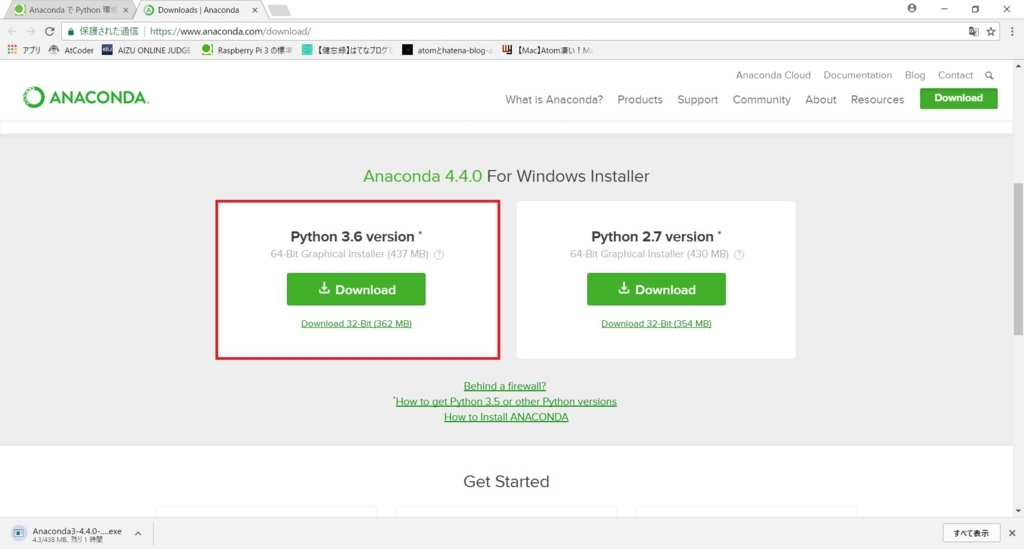
このような画面があると思うので、Python 3.6versionをインストールします。Emailが聞かれますが、No thank youで大丈夫です。



インストーラの起動

インストールが終わったら、インストーラを起動させます。 ほとんどデフォルトのままとしていいのですが、注意点として、最後に以下の2つの項目にチェックを入れましょう。 上は、Anacondaのパスを追加することでコマンドプロンプトからPythonを呼び出すことができます。 下は、デフォルトのPythonを3.6に設定します。 両方にチェックを入れてインストールを開始します。

f:id:ShogoAkiyama:20170906232304j:plain



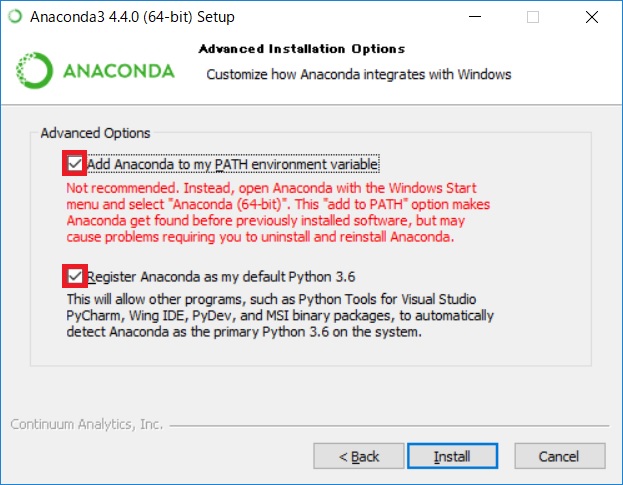
Anaconda Navigatorの起動

無事にインストールが完了したら、実際に起動してみましょう。
左下のWidndowsボタン→Anaconda→Anaconda Navigatorを起動します。

f:id:ShogoAkiyama:20170906232324j:plain



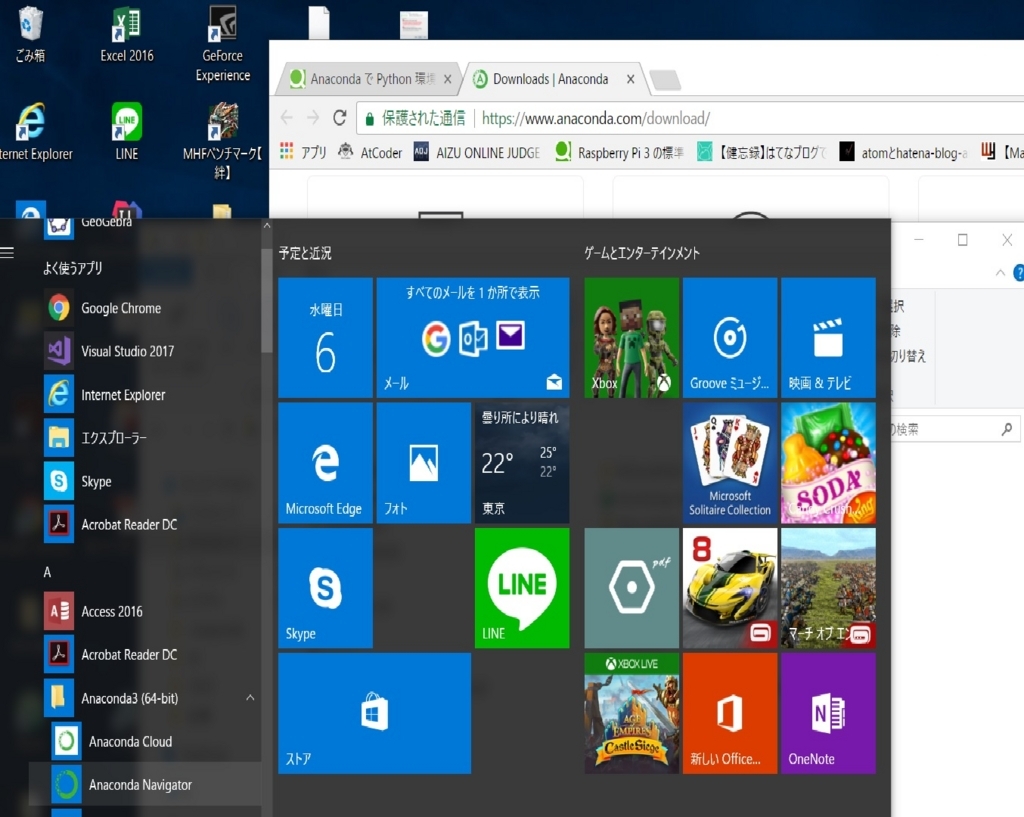
すると、下のような画面が表示されたと思います。 f:id:ShogoAkiyama:20170906232512p:plain 今回は開発環境として、jupyter notebookを使いたいと思います。 （もしも、jupyter Notebookに慣れないようであれば、テキストエディタでPythonコードを書き、Windowsボタン→Anaconda→Anaconda PromptでそのPythonコードを実行することもできます。）



jupyter notebook

f:id:ShogoAkiyama:20170906234828p:plain それでは、jupyter notebookを起動したいと思います。 先ほどの画面のjupyter notebookのLaunchをクリックします。

このような画面が出たと思うので、AnacondaProjectsをクリックします。 f:id:ShogoAkiyama:20170906232740j:plain


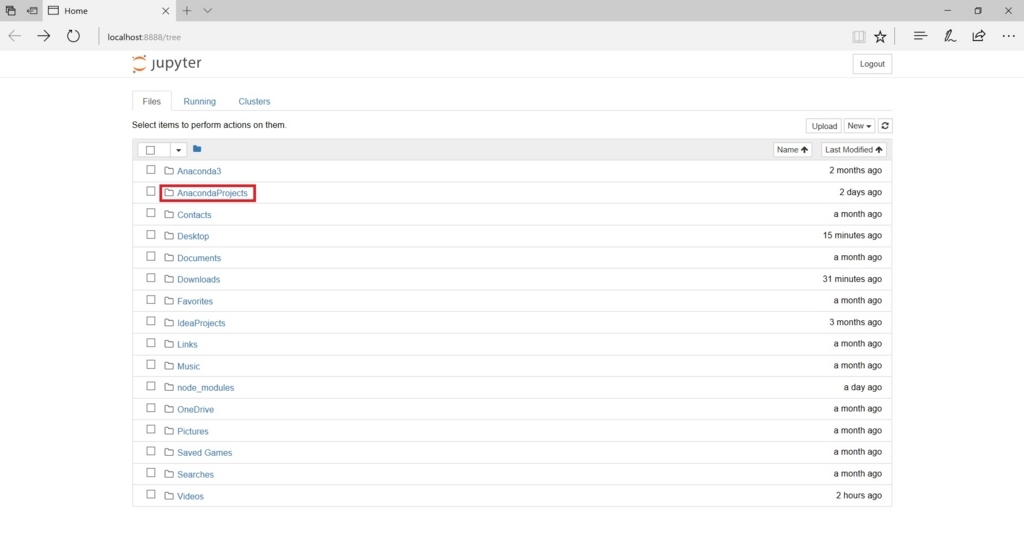
そして、右上にあるNew→Folderから新しいフォルダーを作成します。 f:id:ShogoAkiyama:20170906232801p:plain


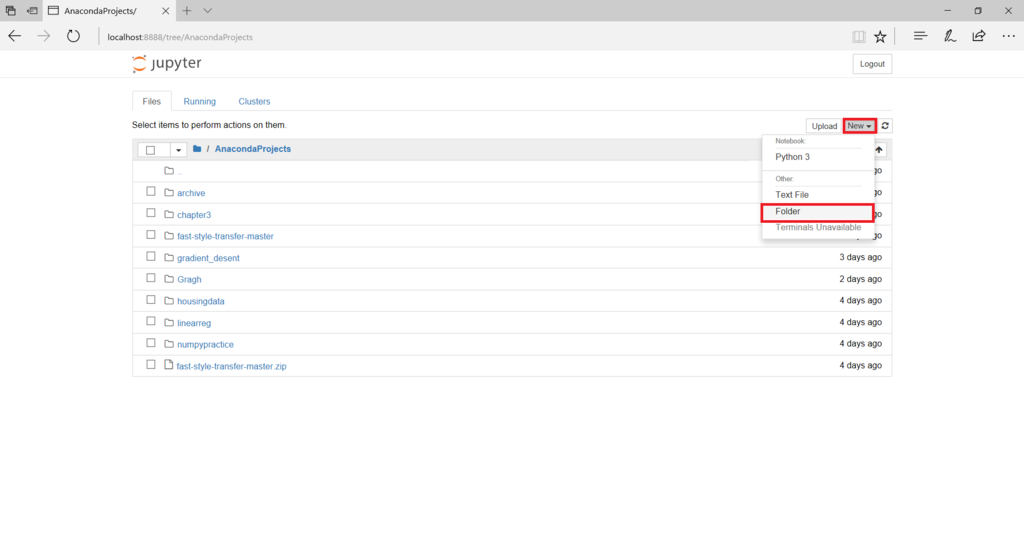
このフォルダーに名前を付けましょう。 新しく作られたフォルダーにチェックを入れ、Renameで名前を付けます。 ここではPractice1と名前を付けました。 f:id:ShogoAkiyama:20170906232836p:plain f:id:ShogoAkiyama:20170906232853p:plain



最後にPythonのファイルを作ります。 右上にあるNew→Pythonをクリックします。すると次のような画面になったと思います。 f:id:ShogoAkiyama:20170906232935p:plain

とりあえず名前を付けましょう。 上のUntitiledと書かれたところをクリックすると、名前を変えることができます。 ここでは、numpy_practiceという名前にします

以上で環境構築が終わりました。 次はjupyter notebookの使い方の説明をしたいと思います。

jupter notebookの使い方 jupter notebookの使い方 - ShogoAkiyama’s blog

確率の基礎

確率・統計

確率変数

コインの表、裏やサイコロの1,2,3,4,5,6など各値に対して、確率が与えられている変数を 確率変数 といいます。

確率分布

ある確率変数 {x} の値が離散であるとき {(x=1,2,‥‥)} 、確率分布は以下のようになります。 f:id:ShogoAkiyama:20170904221100p:plain このグラフを離散型の確率分布といいます。 横軸は確率変数 {x}、縦軸は 確率質量関数 {P(x)} といいます。

また、確率変数が連続{\displaystyle (-∞ \lt x \lt ∞)} であるときの確率分布は、 連続型の確率分布 といいます。 確率変数 {x}が連続の値であるときの確率は 確率密度関数 {P(x)} といいます。

さきほどのグラフではグラフ全体を確率分布と呼びましたが、累積分布関数 {F(x)} のことを分布関数とも呼ぶため、とても紛らわしいです。 累積密度関数はこんな感じのグラフです。 f:id:ShogoAkiyama:20170904225752p:plain

同時確率

2つ以上(ここでは2つ)の確率変数X,Yが与えられたとき、2つの 確率変数の確率を同時確率{ \displaystyle P(x,y) } といいます。

ここからは、以下の表を使って解説していきたいと思います。

1年生 ２年生 ３年生 合計
野球部 0.10 0.15 0.10 0.35
サッカー部 0.15 0.12 0.12 0.39
バスケ部 0.09 0.08 0.09 0.26
合計 0.34 0.35 0.31 1.00

例えば、{X=1年生}、{Y=野球部}の時の{P(X=1年生,Y=野球部)} となる確率は、

{P(X=1年生,Y=野球部)=0.10}

です。 同時確率の合計は確率分布の全ての合計なので必ず1になります。

{ \int_y \int_x P(x,y)dxdy = 1}

周辺確率

確率変数 {x,y}が与えられて、 {x=2年生}だけの確率を求めたいとき、その確率を 周辺確率[tex: {P(x=2年生)} といいます。

ここでは、2年生の合計だけを求めればいいので、 表の2年生の行をすべて足していきます。 $$ \begin{equation} P(2年生) = P(2年生,野球部) + P(2年生,サッカー部) + P(2年生,バスケ部) = 0.35 \end{equation} $$

同様に計算すると、確率変数xの周辺確率は $$ \begin{align} P(1年生) = 0.34 \\ P(2年生) = 0.35 \\ P(3年生) = 0.31 \\ \end{align} $$ となり、 $$ \begin{equation} P(1年生) + P(2年生) + P(3年生) = 1.0 \end{equation} $$ になります。

{ \displaystyle P(x) = \sum_{y} P(x,y)} ( {y}は離散型確率変数)

{ \displaystyle P(x) = \int_y P(x,y)dy} ( {y}は連続型確率変数)

{ \displaystyle P(x,y) = \sum_w \int_z P(w,x,y,z)dz} ( {w}は離散型確率変数, {z}は連続型確率変数)

条件付確率

確率変数 {x,y}が与えられたとき、同時確率は {P(x,y)}と表されましたが、ここで {y}は {y=野球部}から得られたデータであることが分かっていたとします。 このときの確率を 条件付き確率 {P(x|野球部)} いいます。 ここで、同時確率 {P(x,y)}のときは {x,y}のすべての値の合計は1でした。

{ \int_y \int_x P(x,y)dxdy = 1}

条件付き確率では野球部であると分かっているときの確率分布を考えたいということです。ここで、確率分布は合計すると1でなければなりません。 つまり野球部の周辺確率の合計1になるようにしなければならないのです。 野球部の周辺確率は {P(野球部)=0.35} であるため、1になるようにP(野球部)=0.35で野球部の行をすべて割ることで正規化します。

| 野球部 | 0.10 | 0.15 | 0.10 | 0.35 | → | 野球部 | 2/7 | 3/7 | 2/7 | 1 | (割り切れないため分数)

となり、野球部の行を合計すると1になるとうになりました。

よって、条件付き確率は

{ P(x|野球部) = \frac{P(x, 野球部}{P(野球部)} }

となります。

$$ \begin{align} P(w,x,y,z) &= P(w,x,y|z)P(z) \\ &= P(w,x|y,z)P(y|z)P(z) & & (yはzで条件付けられている) \\ &= P(w|x,y,z)P(x|y,z)P(y|z)P(z) & & (xはyとzで条件づけられている) \end{align} $$

ベイズの定理

条件付き確率の式は、 $$ \begin{equation} P(x|y) = \frac{P(x,y)}{P(y)} \end{equation} $$ と表されました。 これを変形すると、 $$ \begin{equation} P(x,y) = P(x|y)P(y) \end{equation} $$ 同様に次の式が得られます。 $$ \begin{equation} P(x,y) = P(y|x)P(x) \end{equation} $$

上の2式を合わせると、下の式ができます。 $$ \begin{equation} P(x|y)P(y) = P(y|x)P(x) \\ ⇔ P(y|x) = \frac{P(x|y)P(y)}{P(x)} \end{equation} $$ これがベイズの定理です。 また、式は {P(y)}は同時確率 {P(x,y)}のあるの点 {x}に注目したと考えれば、 {P(y) = \int_{x} P(x,y)dx}から、 $$ \begin{equation} P(x|y) = \frac{P(x|y)P(y)}{P(y)} \end{equation} $$